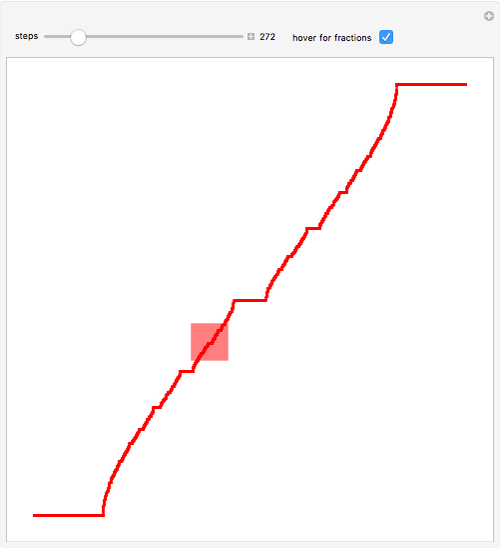
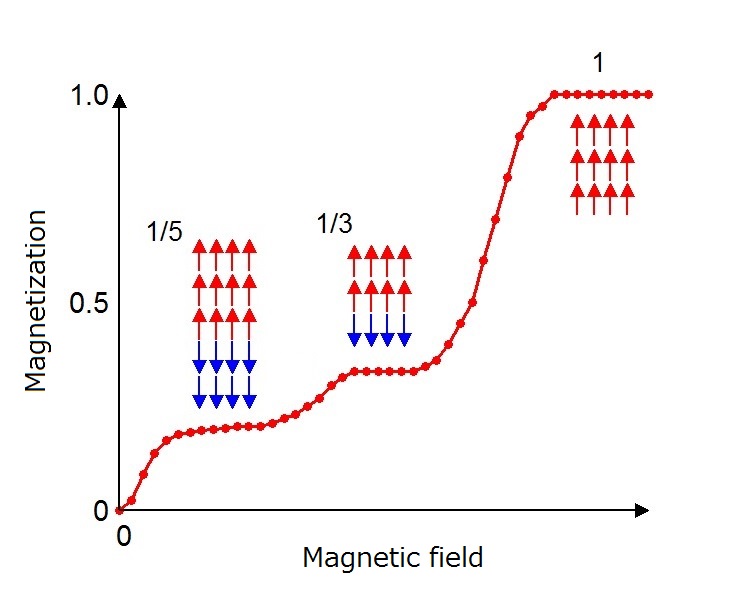
Devil S Staircase Math - • if [x] 3 contains any 1s, with the first 1 being at position n: The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. Call the nth staircase function. The graph of the devil’s staircase. Consider the closed interval [0,1]. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the.
The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The graph of the devil’s staircase. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. Call the nth staircase function. Consider the closed interval [0,1]. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. • if [x] 3 contains any 1s, with the first 1 being at position n: The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third;
Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. Call the nth staircase function. Consider the closed interval [0,1]. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. • if [x] 3 contains any 1s, with the first 1 being at position n: The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The graph of the devil’s staircase.
Devil's Staircase by dashedandshattered on DeviantArt
The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. Call the nth staircase function. The result is a monotonic.
The Devil's Staircase science and math behind the music
Call the nth staircase function. • if [x] 3 contains any 1s, with the first 1 being at position n: The graph of the devil’s staircase. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the.
Devil's Staircase Wolfram Demonstrations Project
The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. Consider the closed interval [0,1]. Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; The devil’s.
Staircase Math
The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. Call the nth staircase function. • if [x] 3 contains any 1s, with the first 1 being at position n: The cantor ternary function.
Devil’s Staircase Math Fun Facts
• if [x] 3 contains any 1s, with the first 1 being at position n: The graph of the devil’s staircase. Consider the closed interval [0,1]. Call the nth staircase function. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps.
Emergence of "Devil's staircase" Innovations Report
Call the nth staircase function. • if [x] 3 contains any 1s, with the first 1 being at position n: The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; The graph of the devil’s staircase. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is.
Devil's Staircase by NewRandombell on DeviantArt
Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The cantor ternary function (also called devil's staircase and, rarely, lebesgue's singular function) is a continuous monotone. The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. [x] 3 =.
Devil's Staircase Continuous Function Derivative
The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; The result is a monotonic increasing staircase for which the simplest rational numbers have the largest.
Devil's Staircase by RawPoetry on DeviantArt
• if [x] 3 contains any 1s, with the first 1 being at position n: Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. The graph of the devil’s staircase. Consider the closed interval [0,1].
Devil's Staircase by PeterI on DeviantArt
The devil’s staircase is related to the cantor set because by construction d is constant on all the removed intervals from the cantor set. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third; The graph of the devil’s staircase. Define s ∞ = ⋃ n = 1 ∞ s.
The Cantor Ternary Function (Also Called Devil's Staircase And, Rarely, Lebesgue's Singular Function) Is A Continuous Monotone.
Define s ∞ = ⋃ n = 1 ∞ s n {\displaystyle s_{\infty }=\bigcup _{n=1}^{\infty }s_{n}}. The result is a monotonic increasing staircase for which the simplest rational numbers have the largest steps. [x] 3 = 0.x 1x 2.x n−11x n+1., replace the. • if [x] 3 contains any 1s, with the first 1 being at position n:
The Devil’s Staircase Is Related To The Cantor Set Because By Construction D Is Constant On All The Removed Intervals From The Cantor Set.
Call the nth staircase function. The graph of the devil’s staircase. Consider the closed interval [0,1]. The first stage of the construction is to subdivide [0,1] into thirds and remove the interior of the middle third;