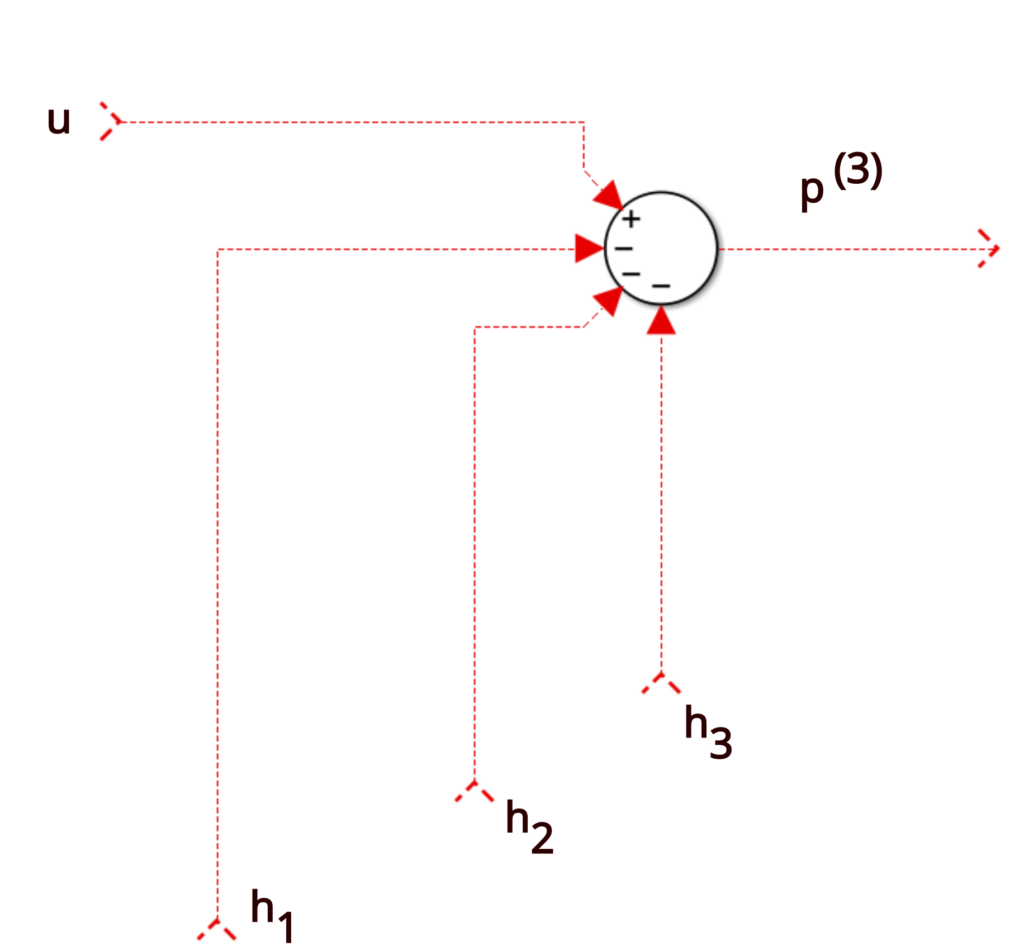
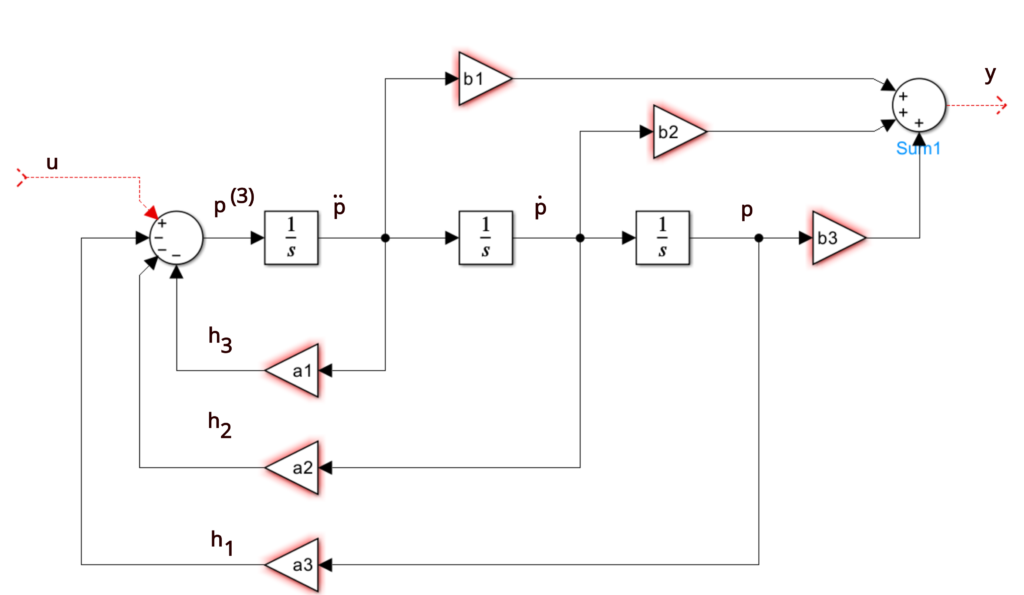
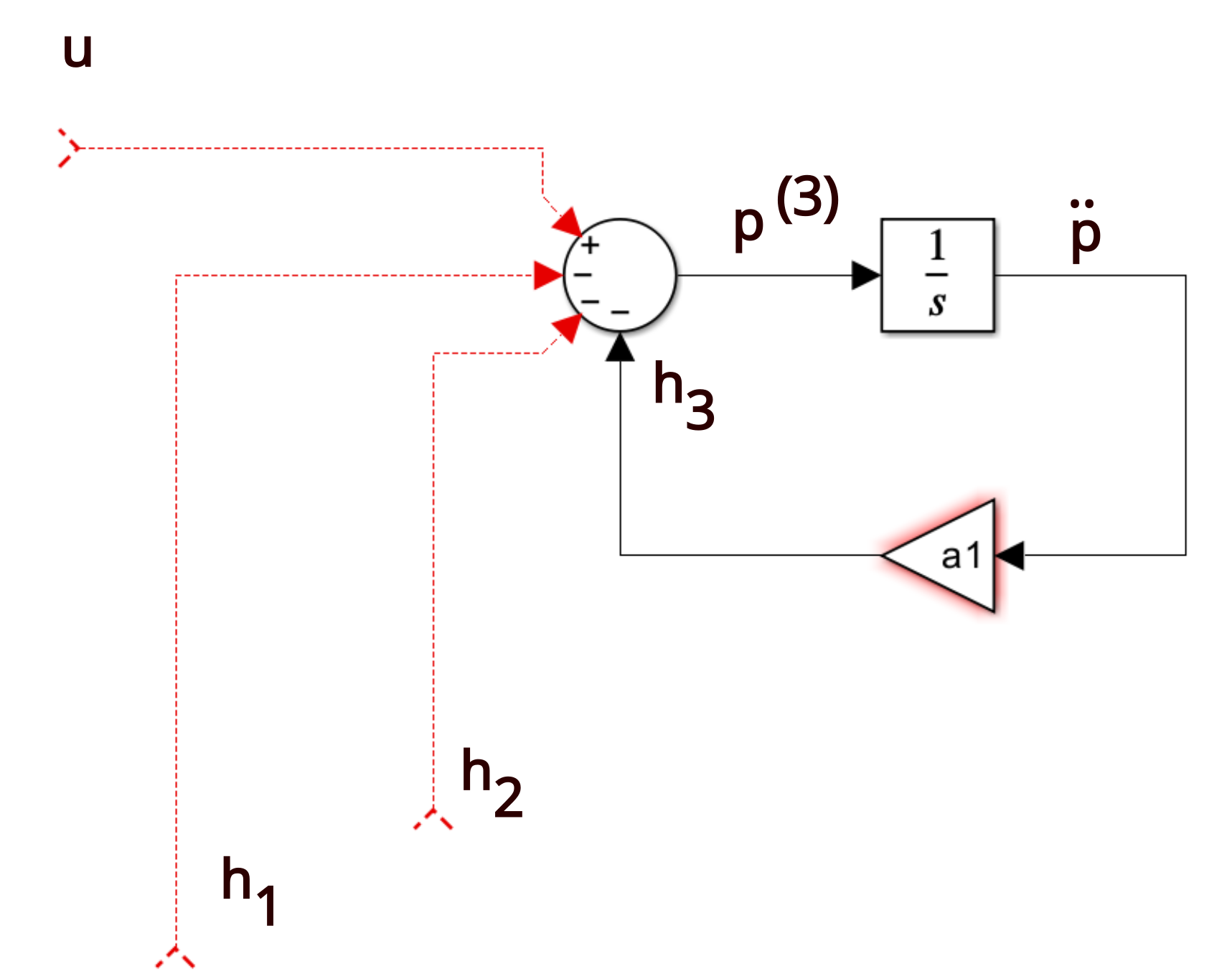
Control Canonical Form - Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. Instead, the result is what is known as the controller canonical form. This is still a companion form because the coefficients of the. Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+.
Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. Instead, the result is what is known as the controller canonical form. This is still a companion form because the coefficients of the. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+.
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This is still a companion form because the coefficients of the. Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. Instead, the result is what is known as the controller canonical form. Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+.
StateSpace Realizations Using Control Canonical Form and Simulation
Instead, the result is what is known as the controller canonical form. Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+. This is still a companion form because the coefficients of the. Two companion forms are.
(PDF) A Jordan control canonical form for singular systems
Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. Instead, the result is what is known as the controller canonical form. Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3.
Solved How to derive mathematically Controllable Canonical
This is still a companion form because the coefficients of the. Instead, the result is what is known as the controller canonical form. Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. Controllability form when a system is in.
Control Theory Derivation of Controllable Canonical Form
Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+. Instead, the result is what is known as the controller canonical form. This is still a companion form because the coefficients of the. Controllability form when a.
EasytoUnderstand Explanation of Controllable Canonical Form (also
Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Instead, the result is what is known as the controller canonical form. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. Canonical_form (xsys, form =.
EasytoUnderstand Explanation of Controllable Canonical Form (also
Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. This is still a companion form because the coefficients of the. Two companion forms are convenient to use in control theory, namely.
Canonical_Form_2 Download Free PDF Eigenvalues And Eigenvectors
Canonical_form (xsys, form = 'reachable') [source] convert a system into canonical form. Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Instead, the result is what is known as the controller canonical form. This is still a companion form because the coefficients of.
Control Theory Derivation of Controllable Canonical Form
This is still a companion form because the coefficients of the. Controllability form when a system is in controllability form, the dynamics have special structure x_ 1(t) = a 11x 1(t) + a 12x 2(t) + b. Instead, the result is what is known as the controller canonical form. Two companion forms are convenient to use in control theory, namely.
Controller canonical form. Download Scientific Diagram
Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This is still a companion form because the coefficients of the. Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1.
EasytoUnderstand Explanation of Controllable Canonical Form (also
Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This is still a companion form because the coefficients.
Controllability Form When A System Is In Controllability Form, The Dynamics Have Special Structure X_ 1(T) = A 11X 1(T) + A 12X 2(T) + B.
Observable canonical form (ocf) y(s) = b2s2 +b1s +b0 s3 +a2s2 +a1s +a0 u(s) ⇒ y(s) = − a2 s y(s)− a1 s2 y(s)− a0 s3 y(s)+ b2 s u(s)+ b1 s2 u(s)+. Instead, the result is what is known as the controller canonical form. Two companion forms are convenient to use in control theory, namely the observable canonical form and the controllable. This is still a companion form because the coefficients of the.